Next: Using EM Up: Modelling Categorical Data: Loglinear Previous: Multinomial logit models through
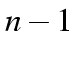 subtables, each consisting of an adjacent pair. Thus we end up
with a table with one binary variable, and an extra dimension
with
subtables, each consisting of an adjacent pair. Thus we end up
with a table with one binary variable, and an extra dimension
with 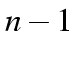 categories. That is, an
categories. That is, an 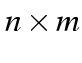 table becomes a
table becomes a
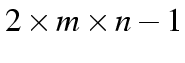 table.
table.
c1 c2 c3
r1 11 12 13
r2 21 22 23
r3 31 32 33
r4 41 32 43
becomes
c1 c2 c3
l1 r1 11 12 13
r1 21 22 23
l2 r1 21 22 23
r1 31 32 33
l3 r1 31 32 33
r1 41 32 43
1 0 281 becomes 1 0 0 281
1 62.5 225 1 0 62.5 225
1 125 283 1 0 125 283
1 250 202 1 0 250 202
1 500 9 1 0 500 9
2 0 1 1 1 0 1
2 62.5 0 1 1 62.5 0
2 125 7 1 1 125 7
2 250 59 1 1 250 59
2 500 132 1 1 500 132
3 0 15 2 0 0 1
3 62.5 17 2 0 62.5 0
3 125 22 2 0 125 7
3 250 38 2 0 250 59
3 500 144 2 0 500 132
2 1 0 15
2 1 62.5 17
2 1 125 22
2 1 250 38
2 1 500 144
treating outcome (normal, abnormal, dead) as ordinal. The first
column is the new variable with 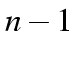 categories, indexing the
new pairs. This can usually be done `by hand' in a text editor or a
spreadsheet, since tables are usually small enough to be convenient.
categories, indexing the
new pairs. This can usually be done `by hand' in a text editor or a
spreadsheet, since tables are usually small enough to be convenient.
GENLOG
outcome BY subtab with dose2
/MODEL=MULTINOMIAL
/PRINT estim /PLOT none
/DESIGN outcome outcome*dose2
outcome*subtab.
where subtab is the index of the subtable.
/DESIGN = outcome outcome*dose2
outcome*subtab
outcome*dose2*subtab.
will allow separate effects.
DOSE OUTCOME COUNT SUBTAB
0 1 281 1 * row 1
62.5 1 225 1
125 1 283 1
250 1 202 1
500 1 9 1
0 2 1 1 * row 2
62.5 2 0 1
125 2 7 1
250 2 59 1
500 2 132 1
0 1 282 2 * row 1 + row 2
62.5 1 225 2
125 1 290 2
250 1 261 2
500 1 141 2
0 2 15 2 * row 3
62.5 2 17 2
125 2 22 2
250 2 38 2
500 2 144 2
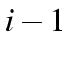 combined. The file
mice-auto.sps
gives an example of doing this automatically within SPSS.
combined. The file
mice-auto.sps
gives an example of doing this automatically within SPSS.
Loglinear Analysis Unit 8
 |
| ||||||||