Next: Multinomial and Ordinal Logistic Up: Sigmoid curves and binomial Previous: Sigmoid curves and binomial
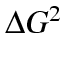 derived in comparing pairs of nested
models does still have a
derived in comparing pairs of nested
models does still have a 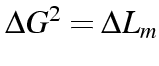 , since
, since
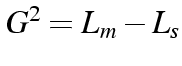
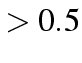 is considered as 1, otherwise zero. This cut
off point is arbitrary, and almost always unsuitable
is considered as 1, otherwise zero. This cut
off point is arbitrary, and almost always unsuitable
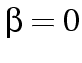
Logistic Regression Unit 2
 |
| ||||||||