Next: The Proportional Odds Model Up: Multinomial and Ordinal Logistic Previous: Multinomial and Ordinal Logistic
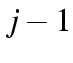 . The default is to
constrain the parameters in these
. The default is to
constrain the parameters in these 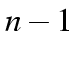 models to be the same:
the effect of the independent variable on being in the higher
rather than the lower of each adjacent pair
models to be the same:
the effect of the independent variable on being in the higher
rather than the lower of each adjacent pair
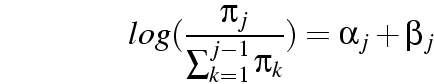
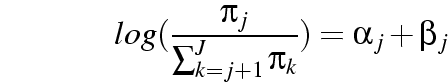
 |
| ||||||||