Does the distribution of one variable differ
across the categories of the other variable?
Examine row or column percentages:
For instance, retirement is the status of 19% of
women but only 16% of men,
for self employment the corresponding figures are 3.5% and
12.3%.
That is, the distribution of employment status clearly
differs by sex (and vice versa).
Association is a non-directional:
row or column percentages equally useful.
If there is no association the variables are said to be
independent. In a table showing independence, the
percentage distributions within any row (or column) will be the
same.
Two unassociated variables
Raw numbers
A
B
Total
I
10
40
50
II
14
56
70
Total
24
96
120
Row percents
A
B
Total
I
20%
80%
50
II
20%
80%
70
Total
24
96
120
Column percents
A
B
Total
I
41.67%
41.67%
50
II
88.33%
88.33%
70
Total
24
96
120
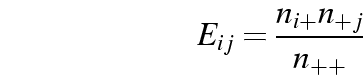
Given a set of marginals (i.e., row and column totals) we
can calculate the expected values under the assumption of
independence according to the following formula:
