Next: The Odds ratio Up: Introduction: the analysis of Previous: Independence
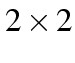 table, a popular
measure is
table, a popular
measure is
| 1 | 2 | Total | |
| 1 | a | b | a+b |
| 2 | c | d | c+d |
| Total | a+c | b+d | a+b+c+d |
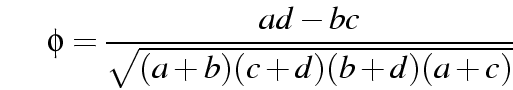
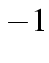 .
.
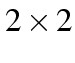 tables it is equivalent.
tables it is equivalent.
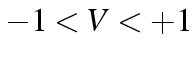 .
.
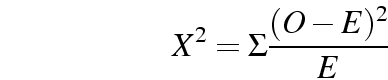
That is, for each cell it calculates a measure of the observed-expected difference, and adds them up.
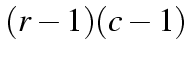 .
.
 |
| ||||||||