Next: Data representations Up: Introduction: the analysis of Previous: Measures of association


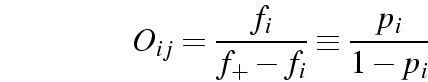
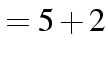 ) of
winning (
) of
winning (
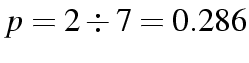 ).
).
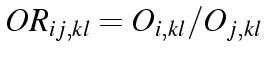
| Owners | Private | Total | |
| renters | |||
| Cons | 1977 | 211 | 2188 |
| Lab | 2353 | 378 | 2731 |
| Total | 4330 | 589 | 4919 |
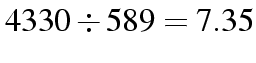 . That is, there are far more owners.
. That is, there are far more owners.
| Conservative |
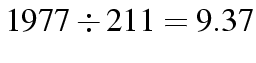 |
| Labour |
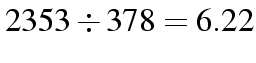 |
| Ratio |
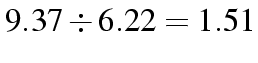 |
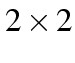 table under independence will have an odds
ratio of 1, whatever the marginals.
table under independence will have an odds
ratio of 1, whatever the marginals.
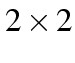 table we can calculate all the cell sizes.
table we can calculate all the cell sizes.
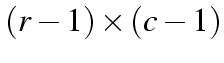 is sufficient).
is sufficient).
 |
| ||||||||