Quasi-Symmetry

• Where marginal homogeneity does not hold, true symmetry is not possible: when a category grows, it is not generally possible for flows out of the category to equal flows into the category, e.g., if there is a swing to Labour this means there are more Conservative to Labour switchers than Labour to Conservative switchers.

• There are models which directly test the hypothesis of marginal homogeneity, but they are not loglinear models and require a different approach to fit (possible with an iterated GLM).

• Where marginal homogeneity does not hold the symmetry model will not fit, but we can test for quasi-symmetry, that is, that there is as much symmetry as possible given the changing marginal distributions.

• To fit this, simply add the row and column variables to the symmetry model:

  genlog avote evote with s2 s3 s4 s5 s6
   /cstructure = offdiag
   /print=est/plot=none
   /design= avote evote s2 s3 s4 s5 s6
  

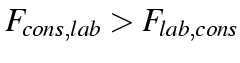• We can interpret this as the independence model with a overlay that says the departure from independence is symmetrical. For instance, after taking account of the fall in the Conservative vote and the rise in the Labour vote (and the net Conservative$\rightarrow$Labour flow arising from this: $F_{cons,lab}>F_{lab,cons}$) there are equal (in the logs) flows from Con to Lab and from Lab to Con.