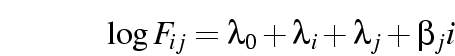- A lot of variables we work with have some ordinality.
- Levels of education, or strength of opinion.
- Some are clearly quantitative, as counts (number of children) or as grouped
continuous variables (age groups, income groups).
- Some have specific values of a variable attached to each
category: school size where categories are different schools,
dose where categories are experimental groups, etc.
- We can model these as nominal and get sensible results but it
is more efficient to take account of the ordinality: we can make
better fitting, simpler models and make stronger claims.
- There are several different approaches to imposing ordinality:
- imposing a linear effect on a variable
- imposing a set on non-linear scores
- calculating a best-fit set of scores
- imposing true ordinality: steps
- Imposing a linear effect simply says that one (or more)
variables has an effect which increases proportionately from
category to category.
- This model suggests that the effect of the row variable can be
approximated by a linear term: There are
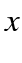 in row 1,
in row 1, 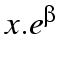 in row 2,
in row 2, 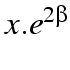 in row three and so on.
in row three and so on.
- If we try this on AOPFAMC by EOPFAMC like
this:
compute alin = aopfamc.
genlog aopfamc eopfamc with alin
/print=est/plot=none/design= eopfamc alin .
we get 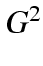 of 6604.7571 for 19 df.
of 6604.7571 for 19 df.
- This model is a constrained version of independence which
says that the
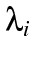 set of parameters can be approximated
by a linear effect. The fit of independence is 1167.1117 for 16,
much better: the row distribution is not well approximated by a
linear effect in this table.
set of parameters can be approximated
by a linear effect. The fit of independence is 1167.1117 for 16,
much better: the row distribution is not well approximated by a
linear effect in this table.
- If we look at the parameter estimates for the
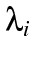 s we
see why a linear effect (of 0.0646) a poor fit:
s we
see why a linear effect (of 0.0646) a poor fit:
i p e
----------------
1 -.4948
2 1.4743
3 2.5569
4 1.9288
5 .0000
- Linear terms become more interesting at higher orders. Here
they impose linearity on the association. If we are classifying
social class by opinion on welfare, it may be plausible that for
a particular category the association effect has a linear form:
very unlikely to agree strongly, very likely to disagree
strongly, with a smooth gradient in between. Each category may
have a different gradient.
- Consider the EVOTE by EOPFAMF table (vote
intention in 1995, by attitude on `Husband should earn, wife stay
at home').
EVOTE Political party supported
by EOPFAMF Husband should earn, wife stay at home
EOPFAMF Page 1 of 1
Count |Strongly Agree Neithr a Disagree Strongly
| agree gree, di disagre Total
EVOTE -----+--------+--------+--------+--------+--------+
1 | 123 | 383 | 538 | 703 | 230 | 1977
Consve | | | | | | 31.4
2 | 214 | 492 | 732 | 1172 | 613 | 3223
Labo | | | | | | 51.1
3 | 39 | 121 | 237 | 302 | 177 | 876
Lib b/SDP | | | | | | 13.9
4 | 10 | 28 | 47 | 82 | 60 | 227
Othe | | | | | | 3.6
+--------+--------+--------+--------+--------+
Column 386 1024 1554 2259 1080 6303
Total 6.1 16.2 24.7 35.8 17.1 100.0
- Independence gives
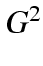 of 100.4906 for 12. If we fit a
linear effect for opinion in association with vote, what happens?
of 100.4906 for 12. If we fit a
linear effect for opinion in association with vote, what happens?
- First, make a copy of the opinion variable. Then enter the
copy as a covariate, and include it in the /design. By
entering a copy as a covariate, SPSS treats the values 1, 2, 3, 4
and 5 as quantitative scores.
compute elin = eopfamf.
genlog evote eopfamf with elin
/print=est/plot=none
/design= eopfamf evote elin by evote.
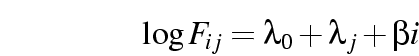
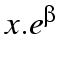 in row 2,
in row 2, 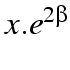 in row three and so on.
in row three and so on.
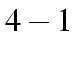 categories of vote.
categories of vote.