Logistic through loglinear

• Since all independent variables are categorical we can treat this data set as a table, and fit the model using loglinear
• This is easiest as a `Loglinear Logit Model' to use SPSS's terms: simply through the Statistics Loglinear Logit menus or with the following syntax:

  GENLOG
    hied BY ageg esex vote
    /MODEL=multinomial
    /PRINT est
    /PLOT NONE
    /DESIGN hied hied*ageg hied*esex hied*vote.
  

  This has new elements:

  • the BY phrase separating the dependent from the independent variables;
  • a multinomial /MODEL; and
  • a design with the dependent variable in interaction with all the independent variables.

• This fits a very large number of parameters, which have a direct relationship to the individual-data logistic regression parameters.

                                                 Asymptotic 95% CI
  Parameter   Estimate         SE    Z-value      Lower      Upper
  
         57     1.6406      .1015      16.17       1.44       1.84
         58      .0000      .            .          .          .
         59    -2.4026      .1463     -16.42      -2.69      -2.12   )
         60    -2.9169      .1037     -28.12      -3.12      -2.71   )
         61    -2.2742      .0913     -24.90      -2.45      -2.10   ) ED*AGEG
         62    -1.7561      .0902     -19.47      -1.93      -1.58   )
         63    -1.1136      .0908     -12.27      -1.29       -.94   )
         64     -.4488      .0985      -4.55       -.64       -.26   )
         65      .0000      .            .          .          .
         . . .
         72      .0000      .            .          .          .
         73     -.3598      .0520      -6.92       -.46       -.26   <--- ED*SEX
         74      .0000      .            .          .          .
         75      .0000      .            .          .          .
         76      .0000      .            .          .          .
         77    -1.0288      .0889     -11.58      -1.20       -.85   )
         78     -.2292      .0785      -2.92       -.38       -.08   ) ED*VOTE
         79     -.8497      .1040      -8.17      -1.05       -.65   )
         . . .
  

• This `Loglinear Logit Model' is simply a special parameterisation of a normal loglinear model which we can fit thus:

  GENLOG
    hied ageg esex vote
    /MODEL=multinomial /PRINT est /PLOT NONE
    /DESIGN hied hied*ageg hied*esex hied*vote
            vote*esex vote*ageg esex*ageg
            vote*esex*ageg vote esex ageg.
  

• This formulation has a more complex model statement and has messier parameter estimates (with this syntax, pairs of estimates have to be subtracted).

• For instance, parameter 59 in the previous model (hied=0 by age-group=1) is parameter 11 (hied=1 by age-group=1) below minus parameter 4 (hied = 0 by age-group=1).

                p.e.        s.e. 
          1     2.0324      .1688      12.04       1.70       2.36
          2     1.6406      .1015      16.17       1.44       1.84
          3      .0000      .            .          .          .
          4     -.1545      .1953       -.79       -.54        .23 <--- ED0*AGEG1
          5     -.1456      .1800       -.81       -.50        .21
          6      .2916      .1742       1.67       -.05        .63
          7      .1595      .1820        .88       -.20        .52
          8      .0062      .1949        .03       -.38        .39
          9     -.5041      .2323      -2.17       -.96       -.05
         10      .0000      .            .          .          .
         11     2.2480      .1953      11.51       1.87       2.63 <--- ED1*AGEG1
         12     2.7714      .1838      15.08       2.41       3.13
         13     2.5658      .1823      14.08       2.21       2.92
          . . .
  

• The exact pattern of parameters that are estimated (rather than marked `aliased') in this syntax depends on their entry order, so sometimes we will find the same effect divided between more than one parameter.

• However, the $G^2$ and fitted values are strictly identical.

• An important point to note is that overall fit of the individual-level logistic regression cannot be judged by the $G^2$; because the number of combinations of different values of variables (``settings'') is very large and a function of the sample, $G^2$ no longer has a $\chi ^2$ distribution. In contrast, $G^2$ for the grouped logistic, or logistic via loglinear, has the usual properties.

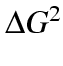• $\Delta G^2$, however, does have a $\chi ^2$ distribution, so pairs of nested models can still be compared.

Loglinear Analysis Unit 7