Everyone knows that Midwinter’s Day, the day of the Winter Solstice, is the shortest day of the year. I think about this a lot, mostly every December/March/June/September (also around DST time changes). A few years ago I discovered the R “suncalc” package. It’s full of interesting astronomical functions, and can show the timing of sunrise, sunset, solar noon and a whole lot of other things, for any date and location. So I’ve been playing with it to help me understand what’s going on.

library(suncalc)
library(ggplot2)
data = getSunlightTimes(date = as.Date(seq(0,32), origin="2023-12-08"), lat=52.7, lon=-8.6)
data$daylength = data$sunset - data$sunrise
ggplot() + geom_point(data=data, aes(x=as.Date(sunrise), y=daylength))

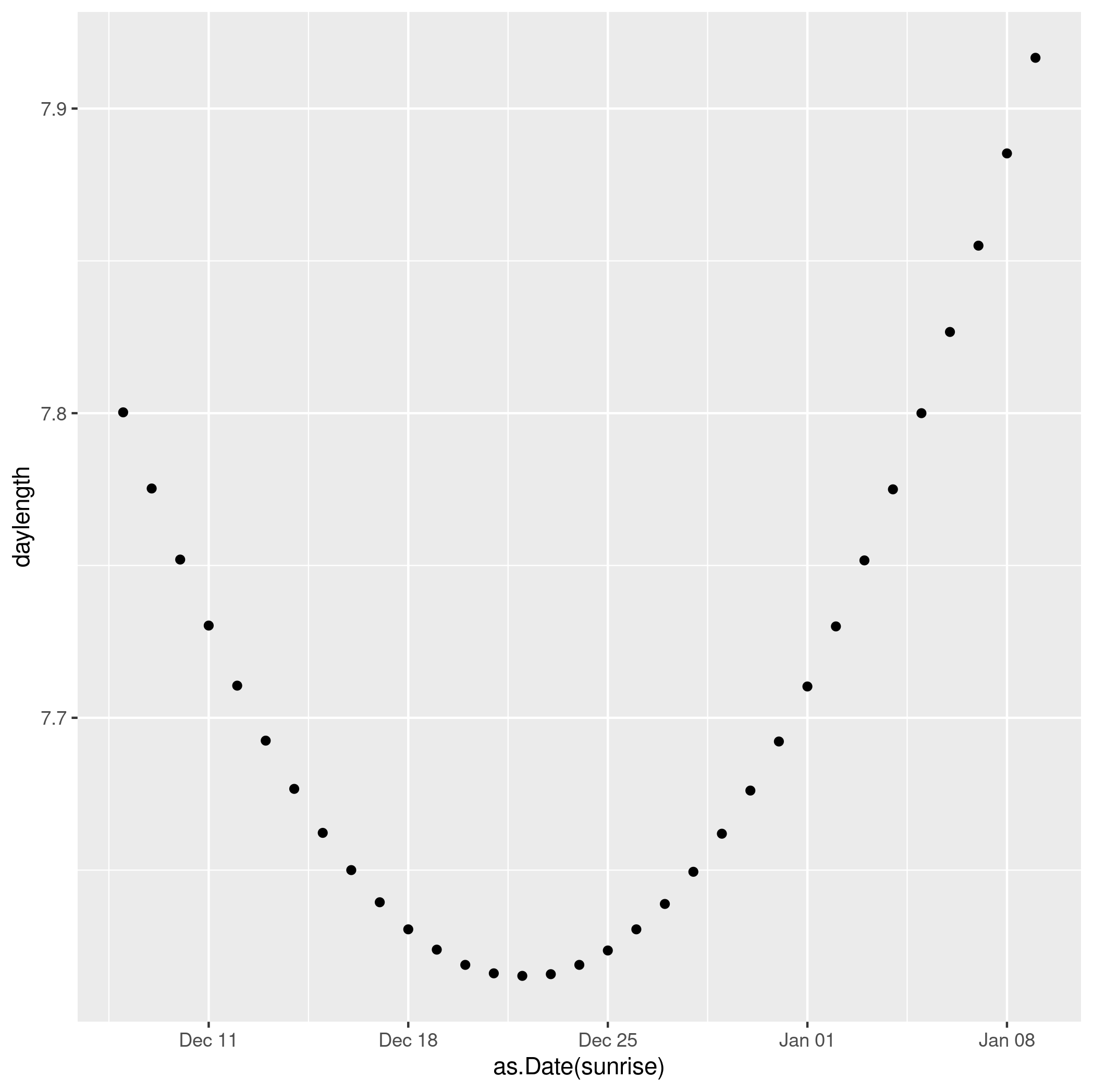
We see clearly that the shortest day in 2023 was Dec 22 (the exact solstice moment was 22 Dec, 03:27).

But the earliest sunset doesn’t actually happen then. It actually happened a few days earlier, Dec 15.

(We Irish are sun-worshippers: https://mastodon.social/@theauldsthretch@mastodon.ie/111585283810569638.)

data$sunsethr = data$sunset - as.POSIXct(as.Date(data$sunset), "00:00:00")
ggplot() + geom_point(data=data, aes(x=as.Date(sunset), y=sunsethr))

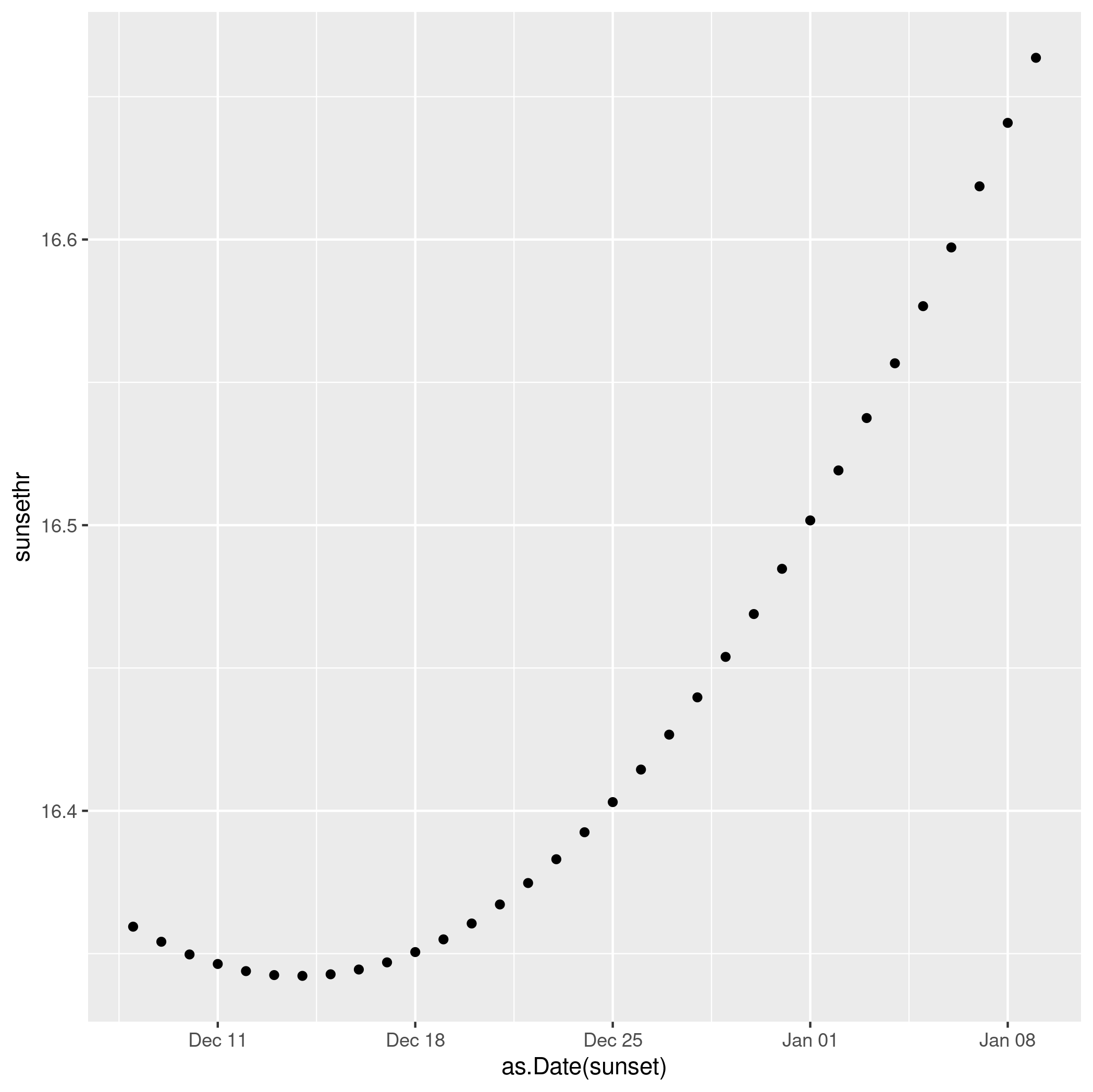
Even more odd, sunrise continues to get later and later until 30 December!

data$sunrisehr = data$sunrise - as.POSIXct(as.Date(data$sunrise), "00:00:00")
ggplot() + geom_point(data=data, aes(x=as.Date(sunrise), y=sunrisehr))

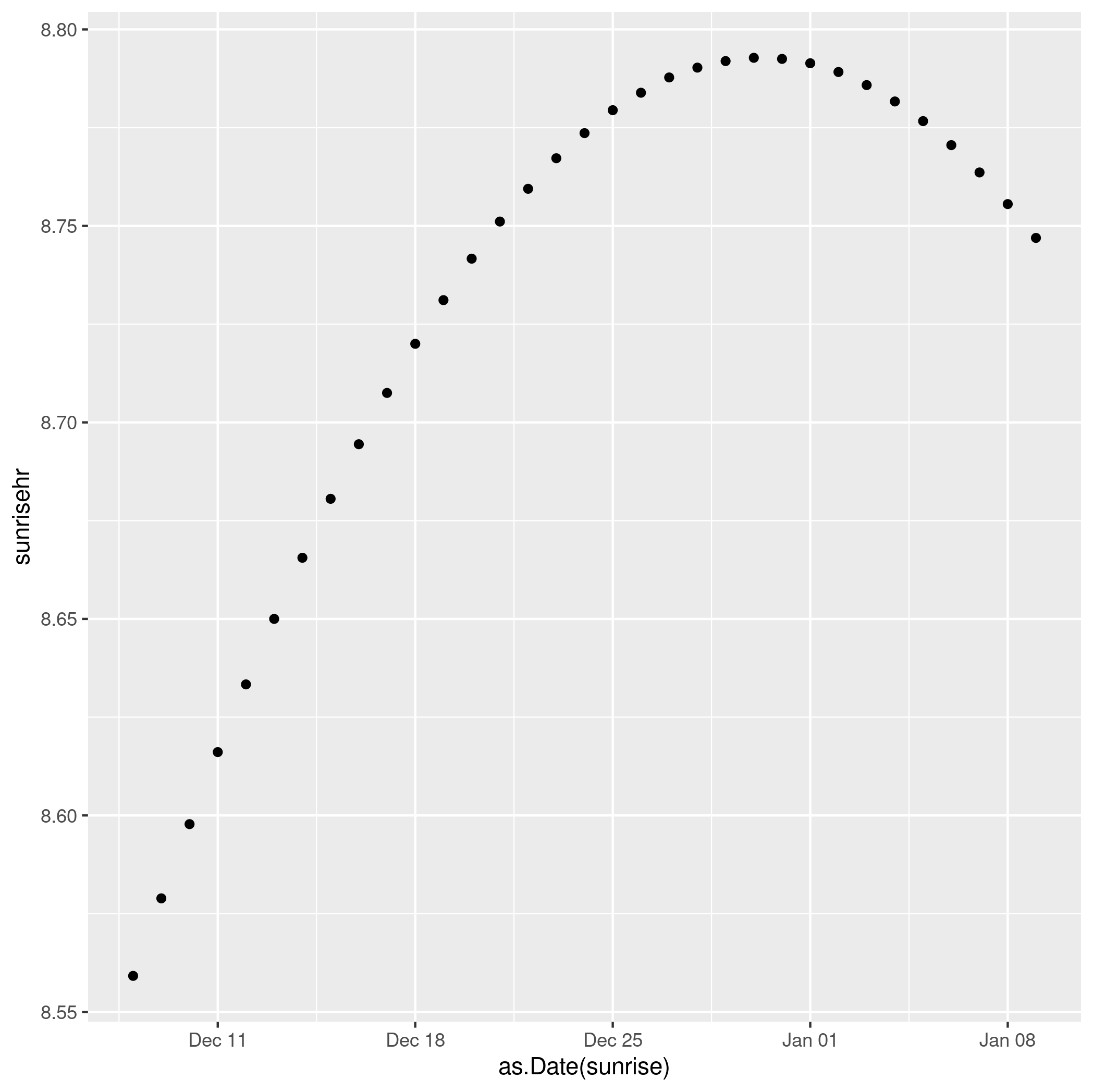
But why doesn’t the shortest day coincide with the earliest sunset and latest sunrise? Surely they should both be equally far from noon? They are, but solar noon and clock noon are not the same. More to the point, the difference between them isn’t constant. In fact, at this time of year it is changing very fast.

data$solarNoonhr = data$solarNoon - as.POSIXct(as.Date(data$solarNoon), "00:00:00")
ggplot() + geom_point(data=data, aes(x=as.Date(solarNoon), y=solarNoonhr))

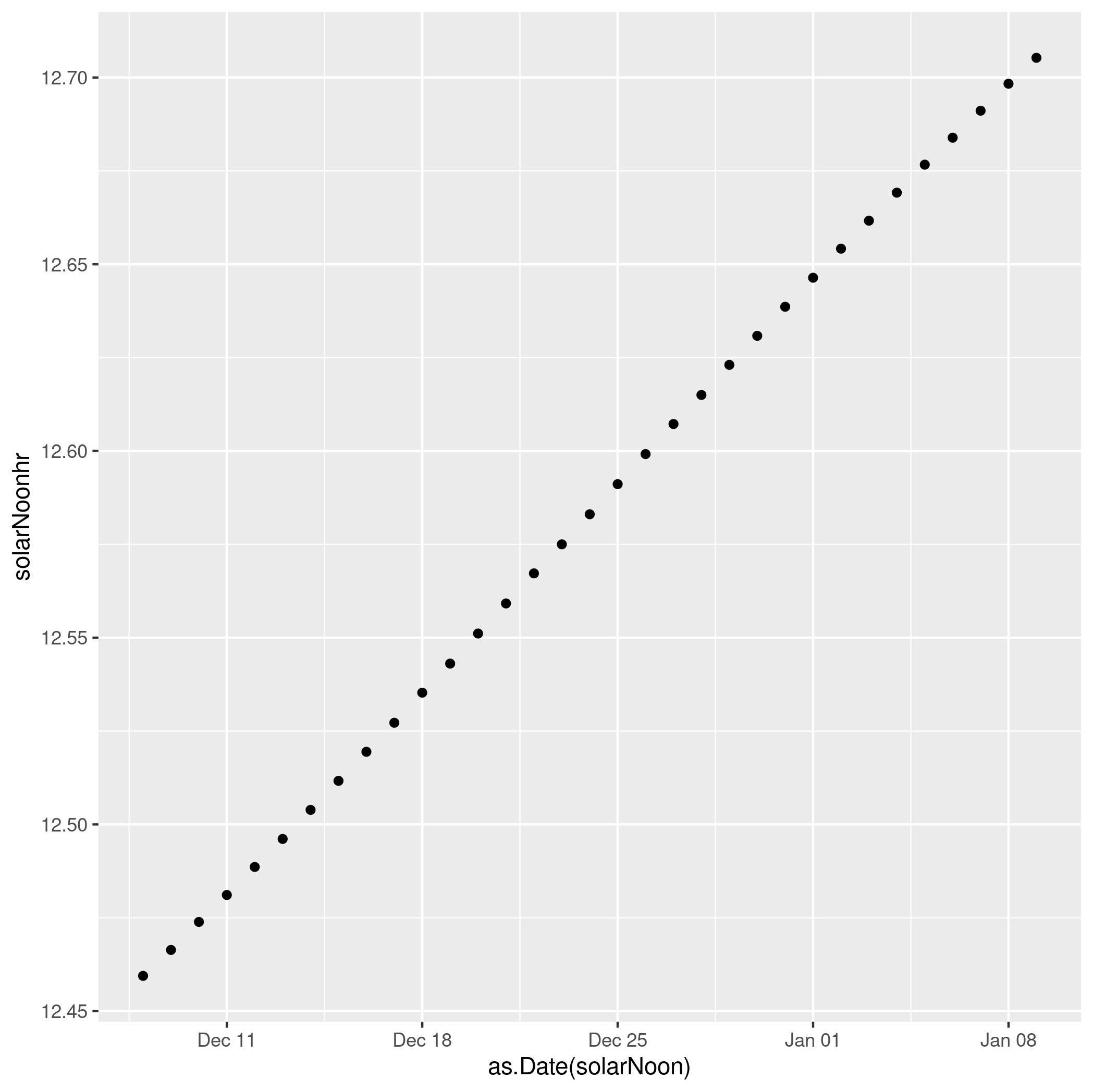
On Dec 8 last, solar noon was at about 12:28 in Limerick. By Jan 9 it will be about 12:43.

It’s due to two factors,the Earth’s elliptical orbit around the sun and the tilt of the Earth’s axis. If the orbit was perfectly circular and the axial tilt zero, the difference would be constant (if on the Greenwich meridian, 0; if at 8.6W as in this example, about 39 minutes). An elliptical orbit means the Earth moves more slowly when further from the Sun, and faster when near. The perihelion, the moment when the Earth is nearest the sun and moving fastest, was only a few days ago: 0038 UTC on 3 January 2024. I’m planning a second post unpicking the axial-tilt and eccentric-orbit effects: watch out for it.

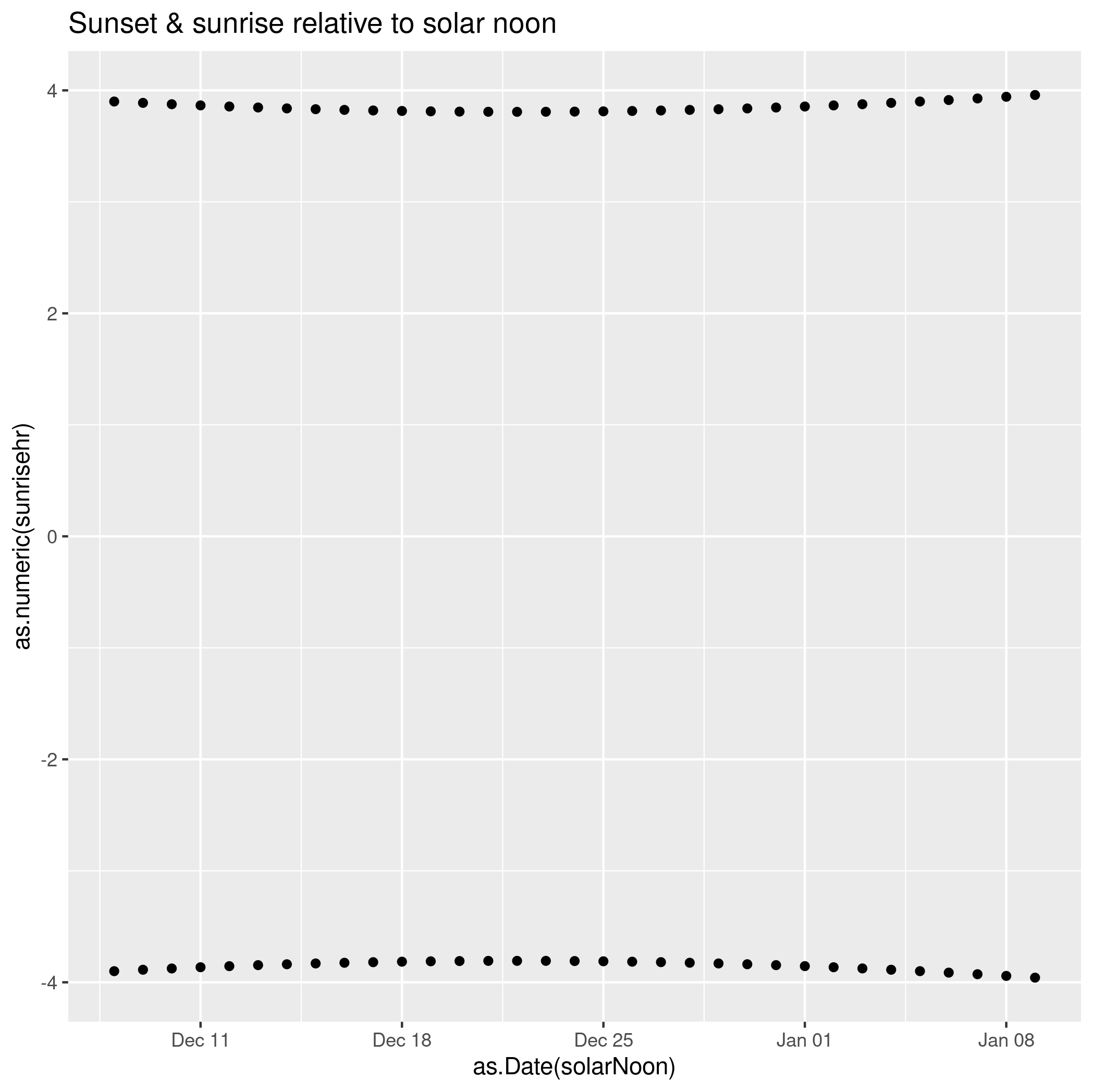
If we look at sunrise and sunset relative to solar noon, if all falls back into place. The day when the sunset is earliest relative to solar noon, and the sunrise is latest, is Dec 22.

data$sunsethr = data$sunset - data$solarNoon
data$sunrisehr = data$sunrise - data$solarNoon
ggplot() + geom_point(data=data, aes(x=as.Date(solarNoon), y=as.numeric(sunrisehr))) +
           geom_point(data=data, aes(x=as.Date(solarNoon), y=as.numeric(sunsethr))) + ggtitle("Sunset & sunrise relative to solar noon")
ggsave("./risesetlength.png")
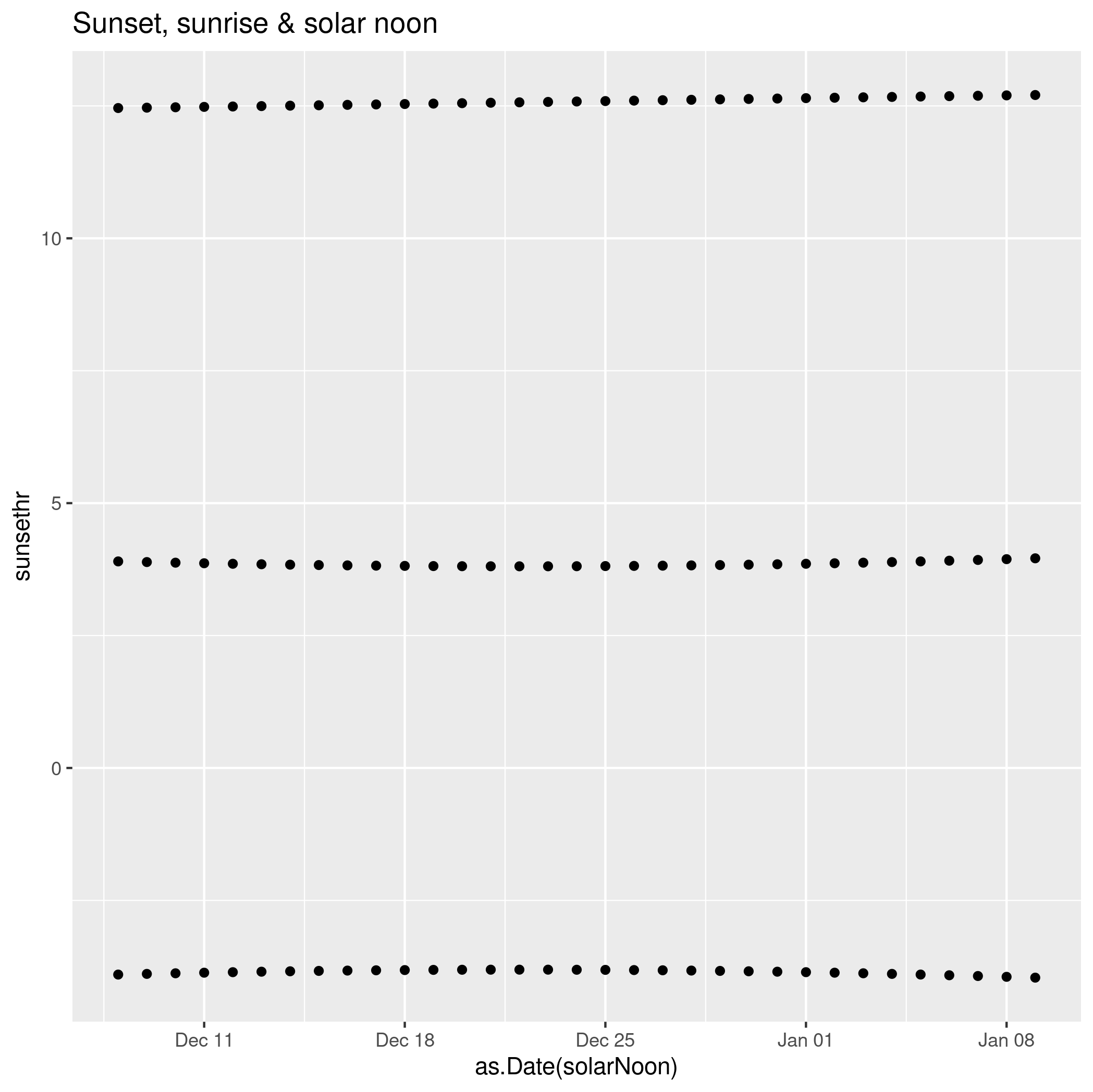
ggplot() + geom_point(data=data, aes(x=as.Date(solarNoon), y=sunsethr)) +
           geom_point(data=data, aes(x=as.Date(solarNoon), y=solarNoonhr)) +
           geom_point(data=data, aes(x=as.Date(solarNoon), y=sunrisehr)) + ggtitle("Sunset, sunrise & solar noon")
ggsave("./solarplus.png")

The point of all this: I wonder about this stuff every solar quarter-day, and the excellent R “suncalc” package (itself based on earlier libraries of astronomical code) is a great way to work out the details. Also, if you live far enough from the equator, you get a bit obsessed with seasonal change in day length!